海星中学校入学試験
来年度より新設される共学スタンダードコースについてご紹介しています。
数学探究講座
11月18日付けブログでもご紹介しましたが、海星ゼミ(講座制授業)では、生徒の皆さんが興味を持つ分野について中学校教育課程の内容を超えて学ぶことができます。
今回ご紹介する「数学探求講座」は、まだ学習していない内容を学ぶものではありません。
必要最小限の数学的知識(中学1年生1学期終了程度)を用いて、論理的思考を磨いていくことを目的としています。
大学入試などで出題された良問を題材に、「問題を解き明かしたい」という欲求をエネルギーに取り組んでいます。

まずは、それぞれが問題に挑戦します。
今回は、[東京大学入試問題(2020文系)]をもとに作ったものです。
ぜひ、挑戦してみてください。
まずは、誘導問題です。
問1 図のように、東西南北に格子状の道が6本交差しています。障害物(●)を交差点に配置すると、道を通行止めにできます。図の●はb-1と表現するものとし、この●によって南北方向のbの道と東西方向の1の道が通行止めになるものとします。このとき、次の問いに答えなさい。
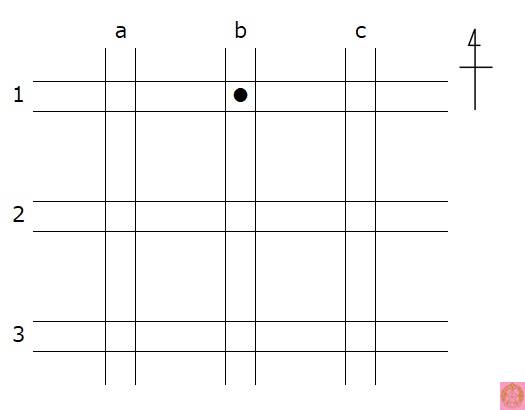
⑴ 6本の道をすべて通行止めにしたいとき、障害物は最低何個必要ですか。
⑵ ⑴の時、障害物の置き方は、全部で何通りありますか。ただし、障害物は区別しないものとします。
⑶ 障害物4個を交差点に配置して、2本の道だけを通行可能にするような置き方は全部で何通りありますか。
ただし、障害物は区別しないものとします。
早く解けた者が説明します。

〈問1の解答〉 ⑴ 3個 ⑵ 6通り ⑶ 9通り
この誘導問題を解決できたら、実際の入試問題の意図を組み入れた次の問いに挑戦です!
問2 図のように、東西南北に格子状の道が7本交差しています。障害物(●)を4個用いて5本の道を通行止めにした上で、2本の道だけを通行可能にしたいとき、障害物の置き方は全部で何通りありますか。ただし、障害物は区別しないものとします。
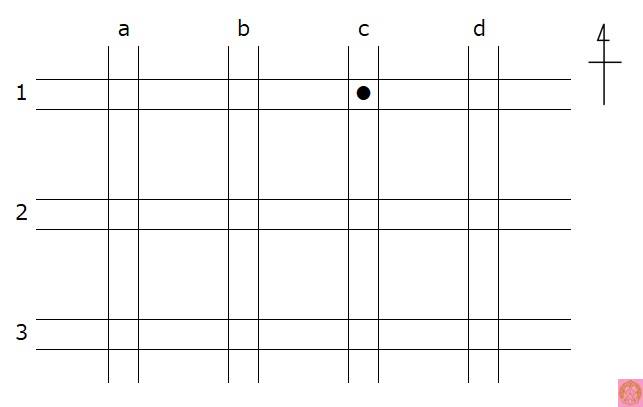
〈問2の解答〉 219通り
実際の入試問題をそのまま出すのではなく、幾つか工夫しました。
工夫① 中学1年生の2学期で学習する座標、及び、中学2年生で学習する直線の式の代わりに障害物と道を用いました。
工夫② 数えやすくするために、交点を16個から12個へ減らしました。
工夫③ 問題をとらえやすくするために、誘導問題として問1を加えました。
受講生全員が誘導問題はできました。
本問である問2を正解したのは1名、正解まであと一歩に迫ったのが2名です。
東京大学の入試問題なんて無理だと諦めるのではなく、まずはやってみることの大切さを本校の生徒は知っています。
これからも海星ゼミ(講座制授業)は、生徒の皆さんの更なる可能性を伸ばす場となっていくことでしょう。


